Binary Trees
Two core traversal techniques:
- Level-order traversal aka Breadth-first search (BFS). Typically implemented with a queue.
- Depth-first search (DFS). Typically implemented with recursion.
- Preorder, inorder, and postorder are three DFS variants (see Binary Tree Traversal)
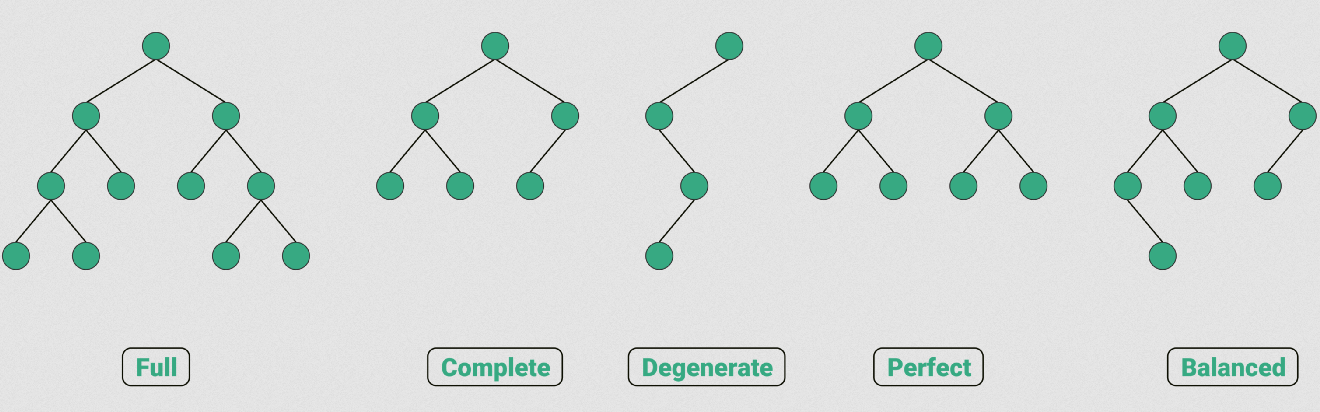
Classes of binary trees:
- Full binary tree - every node has two children
- Perfect binary tree - Full tree with all leaves at the same depth
- Complete binary tree all levels (except potentially last) are full and all nodes are as left as possible
- A (height) balanced binary tree will follow the following conditions:
- The absolute difference of heights of left and right sub-trees at any node at most 1.
- For each node, its left and right sub-trees are balanced binary trees.
Working with binary trees
- Recursive solutions work excellently when conducting DFS on binary trees
- Use a queue when conducting BFS on binary trees
- Complexity analysis on binary trees isn't always straightforward. Focus on left- and right-skewed trees when doing so. If the search space halves each iteration then the complexity is O(log n)
Prototype
class BinaryTreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = rightclass BinaryTreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = rightRust
See this blog post for an introduction to binary trees in Rus
Problems
9.1 Is tree balanced
Resolving the solution for these is sometimes difficult because their solutions are perfectly curated. Understandably they need to be good solutions, but that fact that they're exceptionally condensed makes then terse and hard to read.
I failed to solve this problem, this one, provided in an Inteview may be a deal breaker... unfortunately. I intepreted the problem in a complicated way, not wrong pre-se. What I didn't realize was that I could evaluate each node and whether that node itself had subtrees that were unbalanced.
9.2 tree is symmetric
My solution works, but definitely isn't the most elegant. The trouble is that I lack understanding of how to code a recursive solution, often defaulting to an iterative approach. The key to the iterative approach is to check if the current node value matches one both the left and right side, and then call the check function again on the left and right subtree of both sides. The authors of this book tend to but recursive functions in the functions themselves, instead of making the parent function recursive.
9.4 LCA with parent field
This was a good problem. Successfully got the brute force solution with the Hash Table, which I remembered is a good data structure to compare unordered data. Here the parent is moved up through the chain and each entrie in the hash table has key node and value node.parent. Then we loop through node 2 and check if the current parent node is in the hash table.
The author's solution is comprhesible and elegent. While the Hashtable method techincally makes fewer traverses of the data, it uses O(h) space to store the nodes. Instead if you traverse them at the start to know their depths, you can move up in tandem once you reach the same level and simply compare equality. While the number of passes is greater, is uses O(1) space, and still O(h) time, which is a better trade off. Space is more important than time for optimal solutions.
9.12 Reconstruct a binary tree from traversal data
I only pseudocoded this problem. However the main key insight, I did correctly find, that is, that the first element of the pre-order is the root, and this can be used to find the L and R sub trees, then splitting, and redoing this above step recursively, the solution can be found. My time and space complexity assessments weren't perfect either. My implementation used time complexity O(n^2) since I searched for the index on each subtree. This could have been reduced to O(n) by using a Hash Table to store the index location of each entry with O(1) lookups Keep in mind Hash Table lookups whenever you need to find items in a list or other over and over While this wasn't exactly a perfect solution, I did find the key insights and the code was likely close.
LC 226 Invert Binary Tree
Solution: Use level-order traversal (breadth-first search) with a custom queue, implemented with queue = deque(). Append the root node to the queue, then loop over until it's exhausted. At each iteration, pop the next node off the queue with and. If the node is a None, continue the loop, otherwise swap the left and right sub-trees and append both the sub-trees to the queue. This will visit each node, and in the end reverse the entire binary tree.
- Single loop that traverses to each node of the tree ⇒ $O(n)$ time
- In-place manipulation of the tree with a queue that grows the manage the traversal ⇒ $O(n)$ space worst cast (completely lopsided tree)
LC 110 Is Binary Tree Balanced
This tests you ability to run depth first search with recursion.
Solution: Create a simple depth first search recursive function and give it a signal to operate on. If the signal ever turns false then the tree isn't height balanced.
LC 543 Diameter of a Binary Tree
This question is very similar to the 9.1 Is tree balanced question in implementation. This question tests your ability to traverse a tree structure with recursion, determine the height of left and right sub-trees, and conduct supplementary calculations.
Solution: The key here is the use DFS traversal for counting the height of the tree, and after each left and right sub-tree has been accessed, take the sum of the depths to get the max distance/diameter for that specific node, for example,
class Solution:
def __init__(self):
self.max_diameter = 0
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
def traverse(node) -> int:
if node is None:
return 0
left_depth = traverse(node.left)
right_depth = traverse(node.right)
self.max_diameter = max(self.max_diameter, left_depth + right_depth)
return 1 + max(left_depth, right_depth)
traverse(root)
return self.max_diameterclass Solution:
def __init__(self):
self.max_diameter = 0
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
def traverse(node) -> int:
if node is None:
return 0
left_depth = traverse(node.left)
right_depth = traverse(node.right)
self.max_diameter = max(self.max_diameter, left_depth + right_depth)
return 1 + max(left_depth, right_depth)
traverse(root)
return self.max_diameterAt the end, call travese() with root and the final diameter will be calculated.
LC 104 Maximum Depth of Binary Tree
Solution: Almost identical to the solution above without the need to track the diameter across recursion calls.
LC 113 Path Sum II
This tests your ability to handle a separate data structure while conducting depth-first search on a binary tree.
Solution: Create a stack, and a vector that will hold the result. Conduct depth-first search on a binary tree, at each node pushing the node's value onto the stack if the node is valid. Next, check whether you've encountered a leaf node (left and right sub-trees are null). If so, check that the current sum of the stack matches the target sum and append to the result vector accordingly. At the end of each left/right recursion, pop off the stack so that, at any time, the stack only holds the path to the current node.
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if root is None:
return []
stack = []
result = []
def traverse(node):
if node:
stack.append(node.val)
if node.left is None and node.right is None:
if sum(stack) == targetSum:
result.append(stack.copy())
traverse(node.left)
traverse(node.right)
stack.pop()
traverse(root)
return resultclass Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if root is None:
return []
stack = []
result = []
def traverse(node):
if node:
stack.append(node.val)
if node.left is None and node.right is None:
if sum(stack) == targetSum:
result.append(stack.copy())
traverse(node.left)
traverse(node.right)
stack.pop()
traverse(root)
return result